오늘 알려드릴 내용은 유체역학에서 절대 빠질수없는 내용이에요
레이놀즈 수송정리!
영어로는 Reynolds Transport Theorem, 줄여서 RTT라고합니다
사전지식! Euler해석방법, Lagrange해석방법
RTT를 완전히 이해하기 위해서는 먼저 사전지식이 필요해요
검사체적(Control Volume)과 시스템(System)에 대한 용어를 알아야 하거든요
우리가 어떤 현상이나 물체를 해석할 때, 일정한 질량을 가지는 물체를 가정하고 해석을 진행할 때가 있어요
예를 들면, 질량이 1kg인 공모양 물체를 가정하는것처럼요
공이 굴러가던, 정지해있던 우리는 공만 생각해요
이 공을 검사체적(Control Volume)이라고 하고 이 해석방법을 Euler해석방법 이라고 합니다
우리가 설정한 그 공간에만 관심이 있는거죠
그리고 유체역학만의 또다른 해석방법이 있어요
흘러가는 유체를 추적하면서 그 유체가 어떻게 변하는지를 관찰하는 거에요
추적하는 그 유체를 시스템(System)이라고 하고 이 해석방법을 Lagrange해석방법 이라고 합니다
레이놀즈 수송정리(RTT)는 이 두 해석방법을 이어주는! 정리라고 보시면되요
RTT 유도
그림부터 보실까요?

왼쪽에서 오른쪽으로 흐르는 어떤 유동이 있어요
이 유동장 내에서 두 유선을 설정하고 유동의 방향에 수직인 두 선을 그을거에요
그림에서 하늘색 화살표가 유선, A와 B가 그 수직선이에요
노란색으로 둘러싸인 이 부분을 검사체적(CV), 그만큼의 유동을 시스템(Sys)으로 잡을거에요
이게 초기설정값(t)이에요
그리고 일정시간동안 유동은 이동하겠죠
당연히 시스템(Sys)도 같이 이동할거에요
이 부분을 빨간색 점선으로 나타냈어요
CV만으로 이루어진 구역을 1번 구역,
CV와 Sys가 겹친 구역을 2번 구역,
Sys만으로 이루어진 구역을 3번 구역으로 설정할게요
여기까진 어렵지않죠?
아 한가지를 빼먹었네요
유동은 수직선A를 속도 V1으로 통과하고 수직선B를 속도V2로 빠져나와요
자 이제 제가 말한걸 식으로 써볼게요
복잡하고 이해가 어려울 수 있으니 잘 따라와주세요
시간 t에서 CV와 Sys의 종량적 상태량B은 같아요 그렇게 가정했으니까요
*종량적 상태량에 대한 설명은 용어정리 포스팅에 있습니다*
https://ibeliveicanfly.tistory.com/15?category=869006
[기계공학] 유체역학 용어정리
앞으로 유체역학 주요 내용정리를 해보려고 합니다. 이에 앞서 따로 설명이 필요하거나 중요하다고 판단되는 용어는 여기에 계속 업데이트할 예정입니다. 최근 업데이트 날짜 2021.06.08 유체란? -
ibeliveicanfly.tistory.com

식으로 표현하면 이렇게 되겠네요
일정시간 Δt 가 흐른 후 Sys는 영역CV-1+3을 차지해요

이 식에서 위 식을 빼고 양변을 Δt로 나눠볼게요
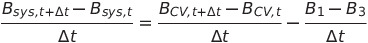
뭔가 생각나지 않으세요?
아직 모르겠다구요? 그럼 양변에 극한을 주면 뭔가 보이실까요?

네, 아주 예전에 배워서 잘 기억은 안나시겠지만
도함수의 정의에요
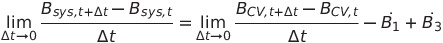
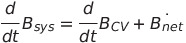
net은 총량, 즉 들어온 B의 양을 뜻해요
이게 RTT의 기본형입니다
하지만 한단계 더 나아갈거에요
여기서 B는 종량적 상태량이니까 B=bm이라는 질량에 관한 식으로 나타낼 수 있어요

마지막 부분이 이해가 안되실거에요
유체에서 '체적'을 설명하는 방법이 하나가 더 있어요

유체가 이렇게 생긴 원통을 지나간다고 가정할게요
유체가 단면적이 A인 원통을 지점1에서 지점2까지 v의 속도로 진행하고 이때 걸리는 시간을 t라고 할게요
그 시간만큼 진행한 유체의 양이 바로 유체의 체적이 되는거에요
그래서

이게 성립이 되는거죠
따라서 시간에 따른 종량적 상태량은

이렇게 표현될 수 있어요
맨 처음에 그림으로 설명할때, [유동이 CV에 수직으로 들어온다]라고 가정을 했었던거 기억나시죠?
하지만 대부분의 유동은 절대 수직하게 들어오지 않아요
그래서 저희는 이제부터 수직성분을 구할거에요
어떻게? 법선벡터와 속도벡터의 내적으로! 수직성분을 구해줄겁니다
검사체적(Control Volume)은 무수히 많은 검사표면(Control Surface)의 적분으로 이루어져 있어요


따라서 RTT의 일반형은!

이렇게 표현되게 됩니다...
아마 이해가 안가는 부분이 많으실거에요
저도 엄청 헤맸던 기억이 있네요
모르시거나 이해가 안가시는부분은 댓글로 알려주시면 더 상세히 설명드릴게요
공부열심히 하세요! :)
'기계공학 > 유체역학' 카테고리의 다른 글
| [기계공학]유체역학 - 원통형 용기 내에서의 회전(강제 와류운동)-2 (0) | 2024.07.14 |
|---|---|
| [기계공학]유체역학 - 원통형 용기 내에서의 회전(강제 와류운동)-1 (0) | 2024.07.05 |
| [기계공학] 유체역학 - 강체 운동 중인 유체3 (0) | 2021.06.22 |
| [기계공학]유체역학 - 강체운동중인 유체2 (2) | 2021.06.21 |
| [기계공학]유체역학 - 강체 운동 중인 유체1 (1) | 2021.06.20 |




댓글