저번 포스팅에 이어 두번째 시간입니다!
원통형에서 회전하는 물에 대한 유체역학이에요
1편을 안보고 오신 분들은 이해가 안될테니
아래 링크로 선 학습하고 오시는걸 추천드립니다!
https://ibeliveicanfly.tistory.com/78
[기계공학]유체역학 - 원통형 용기 내에서의 회전(강제 와류운동)-1
간만에 포스팅하는 것 같네요.. 개인적으로 이직도 하고 여러 사건들이 있어서 미처 신경쓰지 못했는데 여러분들이 댓글을 달아주시는 거에 힘을 얻고! 다시 해보겠습니다! 오늘 알려드릴
ibeliveicanfly.tistory.com
자 그럼 마저 이어서 해볼까요?
오늘은 길지 않아요!
자유표면의 높이 구하기
1편의 포스팅이 자유표면의 높이를 r에 대한 2차식을 마지막으로 마무리를 지어놨었죠
바로 이 식으로요

그런데 왜 또 구하냐?
바로 저 자유표면까지의 거리 hc 때문이에요
측정하기가 굉장히 난해하거든요
그래서 우리는 다른 방식으로 접근해서 저 식을 다시 쓸겁니다!
부피 구하기
원통을 회전시키기 전과 후 물의 부피는 변하지 않아요
시스템으로 더 들어오거나 나간 양이 없거든요

먼저 회전하기 전 부피를 구해보면

당연히 이렇게 되겠죠?
설마 이걸 설명해달라고 하겠어
그럼 회전 후는 어떻게 구할까요?

바로 적분을 사용할거에요
자, 물을 반지름 방향으로 미세하게 쪼개볼게요
그럼

위에서 보면 이렇게 생긴 도넛 모양으로 잘릴거에요
굉장히 미세하게 잘랐으니 도넛의 폭을 dr로 하고 내경을 r로 할게요
그럼 외경은 당연히 r+dr이 되겠죠
그럼 저 도넛의 단면적은

가 될거에요
이렇게 미세하게 쪼개진 도넛기둥(?)을 '쉘' 이라고 표현할게요
이 쉘의 높이는 Zs라고 하겠습니다
여기서 하나 짚고 넘어가야하는 중요한게 있는데
자유표면은 r에 대한 이차식이니 포물선이죠?
그럼 내경r 과 외경r+dr에 대한 높이가 각각 다르겠지만...
우리는 굉장히 미세하게 잘랐기 때문에!
그정도 차이는 무시하고 높이가 같다고 취급합니다
그럼 저 하나의 쉘의 부피는
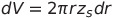
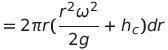
가 됩니다
잘 따라오고 계시죠?
그럼 이제 양변을 적분해볼게요
r의 범위는 0부터 R까지니까
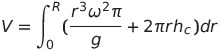
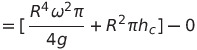
회전 후 물의 부피는 이렇게 될거고
전체 물의 부피는 변하지 않았으니

위 식이랑 이어서 정리해주면 되겠죠?
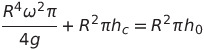
자, 우리가 이걸 하는 이유를 잊어버리면 안돼요
자유표면의 높이를 구하기 어려우니 다르게 접근한거잖아요?
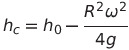
이제 이걸 맨 처음 식

여기에 대입해서 정리하면
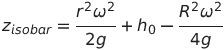
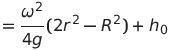
이렇게 됩니다!
오늘은 적분이 나와서 그렇지 저번보다 난이도는 쉬운거에요
그럼 궁금하거나 더 설명이 필요한 부분은 댓글로 알려주시고!
최대한 상세하게 답 해드릴게요
공부 화이팅하세요!
'기계공학 > 유체역학' 카테고리의 다른 글
| [기계공학]유체역학 - 원통형 용기 내에서의 회전(강제 와류운동)-1 (0) | 2024.07.05 |
|---|---|
| [기계공학] 유체역학 - 레이놀즈 수송정리(RTT) (5) | 2021.07.04 |
| [기계공학] 유체역학 - 강체 운동 중인 유체3 (0) | 2021.06.22 |
| [기계공학]유체역학 - 강체운동중인 유체2 (2) | 2021.06.21 |
| [기계공학]유체역학 - 강체 운동 중인 유체1 (1) | 2021.06.20 |




댓글