간만에 포스팅하는 것 같네요..
개인적으로 이직도 하고 여러 사건들이 있어서 미처 신경쓰지 못했는데
여러분들이 댓글을 달아주시는 거에 힘을 얻고! 다시 해보겠습니다!
오늘 알려드릴 내용은 원통형 용기 내에서 회전하는 유체에요
이전 포스팅인 '강체 운동중인 유체 1~3'을 먼저 이해하고 오시기를 권장드립니다
https://ibeliveicanfly.tistory.com/34
[기계공학]유체역학 - 강체 운동 중인 유체1
음..... 이걸 어떻게 쉽게 설명할 수 있을지 모르겠네요 내용이 어렵습니다 하지만 중요하니 설명드려야겠죠 수식이 많고 복잡하고 이해가 안가는 부분이 많을거라 예상해요 최대한 쉽게, 설명
ibeliveicanfly.tistory.com
그럼 시작하겠습니다!
1. 원통형 좌표계
먼저, 조금은 생소한 좌표계를 사용할거라 설명을 드리고 진행해야 할 것 같아요
일반적으로 우리가 쓰는 좌표계는 가로, 세로, 높이로 위치를 표현하는 '직교좌표계'라고 합니다
하지만 이번 주제는 원통형이고, 유체도 원형으로 운동하기 때문에 원통형 좌표계가 좀 더 효율적이에요
x,y,z 대신 반지름r, 각도θ, 높이z 를 사용합니다
그렇다면 압력 P는 r, θ, z에 따라 결정되니

라고 쓸 수 있겠죠
단지 표현하는 문자만 바뀌었을 뿐 계산과정은 똑같으니 어렵지 않습니다!
그럼 시작해보죠
2. 원통형 용기 내에서의 회전

자, 여기 반지름R인 원통형 용기에
높이 h0만큼 유체가 들어있어요
편의상 물이라고 하겠습니다!
가운데 축을 중심으로 회전시키면 저 물은 아마도

이런 모양이 되겠죠?
여기서 물의 높이를 Zs라고 하고 그 최저높이를 hc라고 할게요
먼저, 운동방정식을 살펴보고 들어가야 할거같아요
원통에서 회전하는 물은 각도θ에 대해서 달라지지 않아요 회전축에 대해 모든 각도에서 대칭이니까요
그럼 압력은 각도에 대해 달라지지 않으니

가 되고

이렇게 두 변수에 대해서만 계산하면 되겠네요
양변에 전미분을 해주면



가 되겠죠
여기서 오메가ω는 유체가 회전하는 등각속도를 의미해요
말 나온김에 살펴보자면 구심가속도는

이고 회전운동이라 z방향으로는 아무런 운동도 없으니
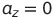
가 됩니다
자, 다시 돌아가서 위에서 썼던 식
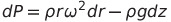
의 양변을 등압면에 있는 점1, 2에 대해 적분해보면
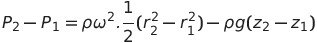
가 되겠죠
점1, 2는 등압면에 있으니
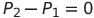
이고 식을 정리하면
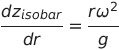
여기서 Zisobar는 임의의 표면에 대한 높이를 말합니다
양변을 r에 대해 닫시 적분하면
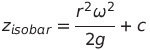
가 되고 여기서 C는 원통 바닥부터 자유표면까지의 거리이니
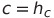
가 될거고 그럼 최종적으로 다시쓰면...!
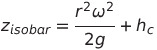
이렇게 자유표면의 높이에 대한 식을 유도할 수 있습니다!
근데 저 식을 잘 보세요
높이 Z는 반지름r에 대한 2차식으로 표현되고 있지 않나요?
맞아요
원통에서 회전하는 물은 등압면에 대해서 반지름에 대해 포물선의 형태를 띄고있습니다!
엄청 신기하지않나요..?
아직 조금 더 남았긴했는데...!
식 유도하는거 따라오는거 힘든거 아니까
나머지는 이후에 또 이어서 포스팅하겠습니다
공부화이팅이에요!
'기계공학 > 유체역학' 카테고리의 다른 글
| [기계공학]유체역학 - 원통형 용기 내에서의 회전(강제 와류운동)-2 (0) | 2024.07.14 |
|---|---|
| [기계공학] 유체역학 - 레이놀즈 수송정리(RTT) (5) | 2021.07.04 |
| [기계공학] 유체역학 - 강체 운동 중인 유체3 (0) | 2021.06.22 |
| [기계공학]유체역학 - 강체운동중인 유체2 (2) | 2021.06.21 |
| [기계공학]유체역학 - 강체 운동 중인 유체1 (1) | 2021.06.20 |




댓글